日誌

日常

メモ

crypt

日誌

日常
  • 下のミスはミスでは無かったようなので計算したら落ち着くべきところに落ち着いた.
  • たまには数論的なオブジェクトと戯れたいと思ったが, 今がまさにそれか. フーリエフーリエ.
  • 新暗号技術(←基礎研究室 2008年度勉強会)
    • えーとまぁなんでCAB暗号を取り上げたのか分からないが, 見つけたのでリンク.
    • まとめのところに書いてある通り, フレームワークもアルゴリズムも紹介されていないので, 今のところ検証不能.

日誌

日常
  • だいたいの場合, 1日に1つでも言いたいことがあれば良いのでtwitterの方で賄えていることよ.
  • 東京には市が沢山あるんだなということを認識した.
  • 計算ミスを発見し, 1つはリカバリしたものの, 1つはリカバリ出来なさそうで困ったところ.

Gentry暗号の簡単な解説

crypt

抽象的なことしか書きません. 詳しいことはACMに$10払うかフルヴァージョンを待つかしましょう.
Gentryの論文は格子の説明が無く初学者に厳しいので, その部分を補うためのノートに使ってください. ただし線形代数と多項式環の知識は仮定します. (といっても学部で習う基本しか使いません.)

暗号方式が3つ出てきますが, 最初の1つだけ気持ちを伝えます.
fを整数係数モニックなn次多項式として環R=Z[x]/f(x)を考えてください. 和と積はZ[x]上で計算してf(x)で剰余を取れば良いです. 更にこの環のイデアルIを1つ持ってきます. 面倒だったらI=(2)とか考えといてください. RとIが共通パラメータです. 公開鍵はIと互素なイデアルJの歪んだ基底Hです. 秘密鍵はこのJの綺麗な基底Bです.
暗号文はコセット m + I の要素 m + i を考えて, c = m + i mod Hです. 復号は綺麗な基底を使って, m + iを取り出して, mod Iを取れば, mが求められます.
なんのこっちゃ.

準備

格子

格子というのは, Z^n中の離散な加法的部分群のことです. なんのこっちゃ. b_1,...,b_n in Z^nが線形独立だとしましょう. B=[b_1,...,b_n]を正方行列として, L = {Bv : v in Z^n} = {\sum_{i} v_i b_i : v_i in Z}ってのが, 格子です. これだと分かり易い. 格子Lに対して, Bのことを基底と言います. そのまんまですね. 1つの格子Lに対して, 基底は無限に存在します. なぜなら, ユニタリ整数要素行列Uを使って, L = {BUv' : v' in Z^n}と書けるからです. まぁ, UはZ^nの線形な1対1写像になっているので良いわけですよ.

多項式環とZ^nの同一視

ベクトル的に考えるのが重要なので, こうしましょう. R=Z[x]/f(x)はZ^nと同一視できます. 具体的には多項式a(x) = a_0 + a_1 x + ... + a_{n-1} x^nをベクトルa = (a_0,a_1,...,a_{n-1})^Tと同一視します. 和はそのまんま. あとZ^{n}の方に対応する積を入れればOKです. これは巡回行列のアイデアを使うと綺麗に書けます. まず, aに対して回転関数を定義します. rot(a) = a(x)・x (mod f)とすればOK. 更に, Rot(a) = [a, rot(a), ..., rot^{n-1}(a)] と定義すると, a(x)・b(x) = a * b = Rot(a)・bと対応が付けられます.

イデアル格子

イデアル格子を定義します. 格子Lがイデアル格子であるとは, Lと同型な環RのイデアルIが存在することです. L = {2Id v: v in Z^n}なんてのはイデアル格子です. なぜなら, 対応するイデアル (2) = {2v : v in R}が存在するから. 逆にイデアルからイデアル格子を定義するのも簡単です. イデアル(a_1,...,a_m)を考えると, 行列[Rot(a_1), ..., Rot(a_m)]とnm本のベクトルを考えて, 適当に直して基底を作って, 格子を作れば良いと.

綺麗な基底と歪んだ基底

GGH暗号方式をMicciancioが改良したもの (CaLC 2001) を思い出します.

鍵生成
秘密鍵は綺麗な基底 B=\sqrt{n}I + R (Rはランダムな小さい要素の行列). 公開鍵はその歪んだ基底H. ここでは, エルミート標準形を使います.
暗号化
平文vを{0,1,2,3}^nの要素とします. 暗号文はc = v mod H.
復号
綺麗な基底Bを知っていると, vが短いベクトルであれば, v mod Hからvに戻せます. 下図を参照のこと.

Gentryの暗号方式その1についてもう1度

簡単に言うとイデアル版Micciancio-GGH+ランダム化です.
平文空間を{0,1}^n mod Iとします. BをイデアルJの綺麗な基底, HをイデアルJの歪んだ基底とします. s in Iを(s)がJと互素になるように選びます. (sは短いベクトル.)
公開鍵は, (R, I, s, H), 秘密鍵はBです.

暗号化
rをRからランダムに選んで, c = m + r s \bmod{H}. これはm + Iというコセットのランダムな要素 m + iをJで剰余を取ったものです. (ただしrが小さい必要あり.)
復号
m = (c \bmod{B}) \bmod{I}. 気持ちとしては, (c mod B)でR上でcをm+rsに戻してやる. 後, mod Iを取れば, rsはイデアルIに含まれるので消えて, m mod Iが求められます. この辺はGGHやNTRUと同じですね.

n次元の絵は描けないので2次元で.
まず, m+rsを考えます.

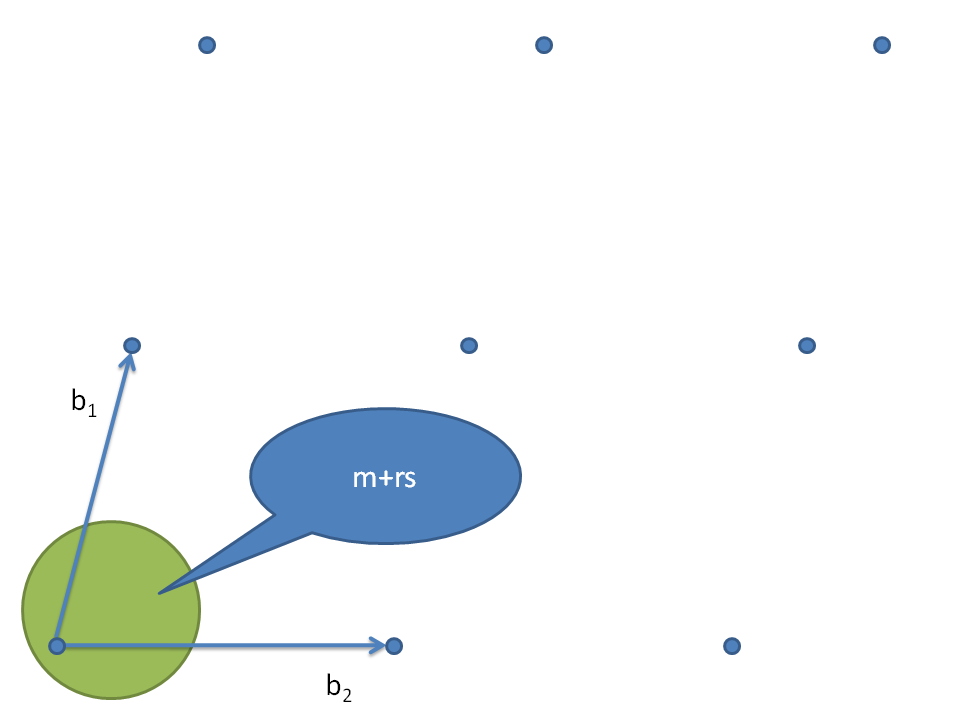
m+rs mod Hだとぐちゃぐちゃ.

m+rs mod Bだと綺麗に四隅に入るので, 戻せそうな気がしてきます. n次元でもm+rsと基底の長さによってちゃんと戻せることが証明できます.

特徴としては簡単に準同型性が言えます.

  • (m + rs) mod H + (m' + r's) mod H = (m + m') + (r + r')s mod H
  • (m + rs mod H)(m' + r's mod H) = (m m' + (m' r + m r' + r r' s) s) mod H

です.
問題は, mとrがそこそこ短くないと復号できないという点です. 足し算したくらいではそんなに長くなりません. しかし, 掛け算すると上の式から分かる通り, 平文ベクトルも乱数ベクトルも長くなります. これを称してエラーが溜まるというわけです.
このエラーの溜まり方は厄介で, 復号回路をシミュレートしようとして和と積を繰り返すと, 結果的に得られる暗号文の平文と乱数が復号できる範囲を超えてしまいます. これは困ったと.

あともう一つの問題は仮定です. R mod H上の一様分布と, rs mod Hが識別不可能という, 決定版CVP問題が難しいことを仮定しています. ちょっと強めの仮定ですね.

解決策

こっからはアブストにあるくらいのことしか話しません.
まず頑張って暗号方式を変形して復号回路の計算量を減らします. がらりと暗号化、復号が変わるのでここ元論文を読んでください. すると深さが減ります. そうなると, 掛算の回数が減るので嬉しいわけです.
KDM安全性を仮定して, (pk1, sk1), (pk2, sk2)を考えます. d = Enc_{pk1}(sk2)が公開されているとします. pk2で暗号化された暗号文e = Enc_{pk2}(m)があったとしましょう. eをもう一度pk1で暗号化すると, e~ = Enc_{pk1}(e)です. これとdを使うと, pk2側の復号回路がpk1側でシミュレート出来ならば, e~ = Enc_{pk1}(m)が計算できます. Enc_{pk1}関数が新しく追加するエラーが小さければ, これを繰り返し行うことでいろいろ出来そうなわけです.

返信

crypt

期待されているようなので, Gentryの暗号 (STOC 2009) については簡単な解説を後日書きます. 今のところフルヴァージョンは公開されていないので, 詳しいテクニックはぼかして書く方向で.
乗法的準同型性, 加法的準同型性, 制限付き加法的準同型性, 制限付き環準同型性, 制限無し環準同型性辺りといった歴史を押さえて書いた方が良いか. 30年来の未解決問題でもあったことだし.

ものすごい大雑把に言うとNTRUとGGHの拡張みたいなもんです. アイデアはそっちに近い.
ただこれだけだとANDやORの素子を評価するたびにエラーが溜まっていくので, 一旦内部で復号してエラーをキャンセルします. そのために最近流行のKDM安全性を仮定して, 秘密鍵を暗号化してそれを公開鍵に含めておく. すると, 復号回路をエミュレート出来るというアイデアです.

あと取り急ぎ指摘しておくと,

  • Applebaum, Cash, Peikert, and Sahai (CRYPTO 2009) のは関連あるっちゃありますけど, 直接的では無いです.
    • これの主題は, LWE仮定からKDM-secureな公開鍵暗号方式, LPN仮定からKDM-secureな秘密鍵方式, LPN仮定から線形伸長可能な擬似乱数生成器とかです. 計算量が低い点とKDM安全性は共通しています.
  • Cloud(SaaS)に任せられる仕事とは何か - kgbu?
    • イデアルの束(Lattice)と訳されていますが, これはイデアル格子が正しいです. latticeと言ったときには科学としては二つの訳があり, 束と格子です. この場合は格子が正解.

正しいアブストラクトの訳は以下.

アブスト和訳

完全な環準同型性を持つ公開鍵暗号方式 -- すなわち、 復号することなく、データの暗号文のみから、データを回路に入力したときの出力の暗号文を得ることが出来る方式 -- を提案する。解決策は3段階に分かれる。まず、一般的な結果を示す。任意の回路の評価を許す暗号化方式を構成するためには、（多少拡張した形の）自身の復号回路を評価できれば十分であることを示す。このように（拡張）復号回路を評価可能な暗号化方式のことを「ブートストラップ可能である」と呼ぶ。

We propose a fully homomorphic encryption scheme -- i.e., a scheme that allows one to evaluate circuits over encrypted data without being able to decrypt. Our solution comes in three steps. First, we provide a general result -- that, to construct an encryption scheme that permits evaluation of arbitrary circuits, it suffices to construct an encryption scheme that can evaluate (slightly augmented versions of) its own decryption circuit; we call a scheme that can evaluate its (augmented) decryption circuit bootstrappable.

次に、ほぼブートストラップ可能である、イデアル格子を用いた公開鍵暗号方式について説明する。

Next, we describe a public key encryption scheme using ideal lattices that is almost bootstrappable.

格子ベースの暗号方式は、復号の回路計算量が低い。大抵の場合、NC1*1に含まれる内積の計算が主である。また、イデアル格子を用いることで加法的準同型性と乗法的準同型性が導入される。これらの準同型性は、多項式環中の格子として表現された公開鍵として用いられるイデアルを法に取る。また、これらの準同型性は一般の回路を評価する際に必要である。

Lattice-based cryptosystems typically have decryption algorithms with low circuit complexity, often dominated by an inner product computation that is in NC1. Also, ideal lattices provide both additive and multiplicative homomorphisms (modulo a public-key ideal in a polynomial ring that is represented as a lattice), as needed to evaluate general circuits.

残念ながら、最初の方式はブートストラップ可能ではない。格子の次元のログオーダーの深さで表現される回路のみ正しく評価可能である。復号回路の深さも格子の次元のログオーダーであるが、これは評価可能な回路の深さよりは大きい。従って、最終ステップでは、評価出来る回路の深さを減らすことなく、復号回路の深さを減らすためにいかに方式を変更するかを示す。抽象的に言えば、復号化の計算量を減らすために暗号化の際に復号の一部を行う。これはserver-aided暗号方式 *2 で、 サーバが復号化の一部を行うことと非常に似ている。

Unfortunately, our initial scheme is not quite bootstrappable -- i.e., the depth that the scheme can correctly evaluate can be logarithmic in the lattice dimension, just like the depth of the decryption circuit, but the latter is greater than the former. In the final step, we show how to modify the scheme to reduce the depth of the decryption circuit, and thereby obtain a bootstrappable encryption scheme, without reducing the depth that the scheme can evaluate. Abstractly, we accomplish this by enabling the encrypter to start the decryption process, leaving less work for the decrypter, much like the server leaves less work for the decrypter in a server-aided cryptosystem.

*1:2入力AND, OR, NOTからなる多項式サイズかつ深さがO(log n)の回路で判定可能な計算量クラス. 参考:Complexity Zoo:N - NC1

*2:これの定訳なんだっけ?

最近の格子ネタ

crypt
  • お久しぶりです.
  • C. Gentry. “Fully homomorphic encryption using ideal lattices.” (STOC 2009)
    • えーとね, あんまり細かく読む気が起きてないんだけど. 安全性に関してはぱっと見それNTRU以下だろうという感じ. どうなんだろうね.
    • うーん, mod qを取らないNTRUというかGGHというか. ちょっと真面目に考えよう.
    • KDM安全性を仮定すると回路をエミュレート出来るってのはいいですね. これは使えそう.
    • ただKDM安全性がきついなぁ.
  • D. Stehlé, R. Steinfeld, K. Tanaka, K. Xagawa “Efficient Public Key Encryption Based on Ideal Lattices.” (ePrint 2009/285)
    • これもあんまり読んでないけどね.
    • Gentry, Peikert, and Vaikuntanathan (STOC 2008) とPeikert (STOC 2009) のイデアル格子版.
      • 基底生成にはAlwen and Peikert (STACS 2009) ではなくて, Ajtai (ICALP 1999) を使っている.
      • Regevの量子帰着もPeikertの古典帰着もそのままでは使えないので, 一回SISに帰着するというテクニック.
      • あとIDベース認証と署名の話もついてる.
      • IND-CCA2もやってるみたい.

あとは, WEWoRCでダルムシュタット系の人たちが2本分くらい話すようです.